Arcsine Calculator

The arcsin function, also known as the inverse sine function, is a mathematical operation that allows us to find the angle whose sine is equal to a given value. It is the inverse of the sine function and is denoted as arcsin(x) or sin^-1(x).

\begin{aligned} \arcsin({1}) &=\; 1.570796327 \; \text{rad} \\ &=\; 90 \degree \end{aligned}

Created by Wes Nolte.Last updated Apr 25, 2024.

The Arcsine Calculator Formula

y = \arcsin(x) = \sin^{-1}(x)

Definition of the Arcsine Function

Arcsine, commonly denoted as asin or sin⁻¹, is a fundamental function in trigonometry and calculus. It's the inverse of the sine function, which means it operates in reverse to find the angle when the sine of that angle is known. The sine function, which relates the ratio of the length of the opposite side to the hypotenuse in a right triangle, is one of the primary trigonometric functions. When you have a value for the sine and you want to determine the corresponding angle, you use the arcsine function.The domain of the arcsine function is limited to the range [-1, 1], as these are the minimum and maximum values the sine of an angle can achieve. The output, or range, of the arcsine function is typically restricted to angles between -90° and 90° (or -π/2 and π/2 in radians). This restriction is necessary because the sine function is not one-to-one; each sine value corresponds to multiple angle values. By limiting the range of the arcsine function, it ensures that each input (sine value) corresponds to exactly one output (angle).The output of the arcsine function can be expressed either in radians or degrees because these are two standard units of measuring angles, each with its own context and application. Degrees, a more intuitive and historically older system, divide a full circle into 360 parts, making it easy to relate to everyday concepts. This system is often used in education, navigation, and various fields where simplicity and tradition are important. Radians, on the other hand, are the standard unit in mathematical and scientific contexts due to their natural relationship with various mathematical concepts. In radians, the measure of an angle is directly related to the length of the arc it subtends on a unit circle. One full circle is 2π radians, linking angular measurements to the properties of circles and enabling simpler and more elegant formulas in calculus and trigonometry. The choice between radians and degrees depends on the specific requirements of the field or problem at hand, with radians favored for theoretical work and degrees for practical applications.

Arcsine Example

Imagine you're an engineer working on the design of a new ramp for a warehouse. The ramp must be gentle enough for safe use but steep enough to be practical. You decide that the maximum incline of the ramp should not exceed a slope of 30%. Slope is defined as the ratio of the rise (vertical height) to the run (horizontal length) of the ramp.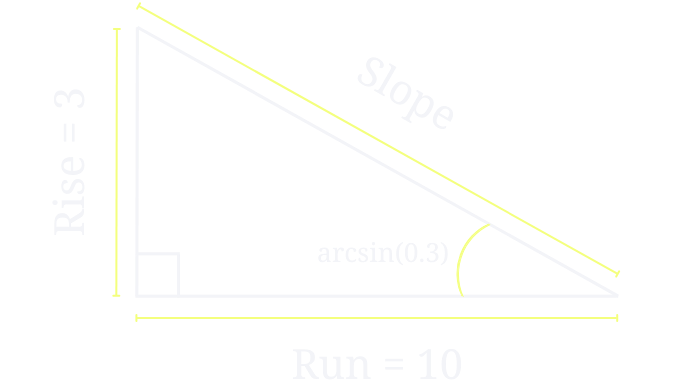 Arcsine calculation example

To find the maximum angle at which to build the ramp, you can use the arcsine function. Here's how:

First, convert the slope percentage into a decimal. A 30% slope is 0.30 in decimal form (since 30% = 30/100 = 0.30).
This slope ratio is essentially the sine of the desired angle. In a right triangle, the sine of an angle is the opposite side (rise) over the hypotenuse (the slope length). In this case, the rise/run ratio is 0.30.
To find the angle, you use the arcsine function: $ext{Angle} = arcsin(0.30)$
You can then calculate this using a calculator set to the appropriate mode (degrees or radians, depending on your needs).

For instance, if you're working with degrees: $ext{Angle} = arcsin(0.30) approx 17.46^circ$

This result tells you that the maximum angle of your ramp should be approximately 17.46 degrees to maintain the desired 30% incline.

Arcsine Lookup Table

Below is a table of commonly use values in calculating Arcsine.

y	x = arcsin(y)
y	degrees	radians
-1	-90°	-π/2
-0.8660254	-60°	-π/3
-0.7071068	-45°	-π/4
-0.5	-30°	-π/6
0	0°	0
0.5	30°	π/6
0.7071068	45°	π/4
0.8660254	60°	π/3
1	90°	π/2